数学基础P1-P6
数学基础 P1-P6
1. 向量
1.1 定义
几何定义:
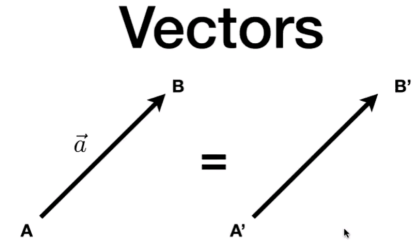
$\vec{a}=\vec{AB}=B-A$
几何意义:
长度 $|\vec{a}|$ 向量的模
方向 $\hat{a}=\vec{a}/|\vec{a|}$ 单位向量数学定义

向量矩阵 $A=\pmatrix{x\y}$
转置矩阵 $A^T=(x,y)$
矩阵的模 $|A|=\sqrt{x^2+y^2}$
1.2 运算
1.2.1 加法运算
- 几何学
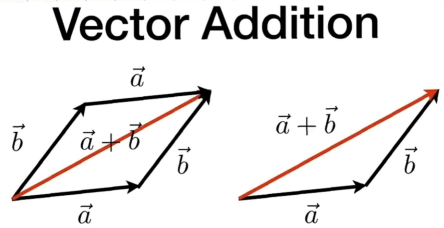
四边形法则与三角形法则 - 数学
$A=\pmatrix{x_{A1}\y_{A2}}$ $B=\pmatrix{x_{B1}\y_{B2}}$
$A+B=\pmatrix{x_{A1}+x_{B1}\y_{A2}+y_{B2}}$
运算结果:新向量
1.2.2 点乘
几何学
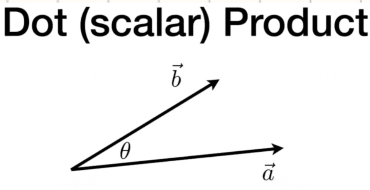
$\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|cos\theta$
一般向量:$cos\theta=\cfrac{\vec{a}\cdot\vec{b}}{|\vec{a}||\vec{b}|}$
单位向量: $cos\theta=\hat{a}\cdot\hat{b}$适用规则:
- 交换律 $\vec{a}\cdot\vec{b}=\vec{b}\cdot\vec{a}$
- 分配律 $\vec{a}\cdot(\vec{b}+\vec{c})=\vec{a}\cdot\vec{b}+\vec{a}\cdot\vec{c}$
- 结合律 $(k\vec{a})\cdot\vec{b}=\vec{a}\cdot(k\vec{b})=k(\vec{a}\cdot\vec{b})$
数学
- 2D:$\vec{a}\cdot\vec{b}=\pmatrix{x_a\y_a}\cdot\pmatrix{x_b\y_b}=x_ax_b+y_ay_b$
- 3D:$\vec{a}\cdot\vec{b}=\pmatrix{x_a\y_a\z_a}\cdot\pmatrix{x_b\y_b\z_b}=x_ax_b+y_ay_b+z_az_b$
运算结果:数字
应用:
计算两向量夹角(光线反射角)
$cos\theta=\cfrac{\vec{a}\cdot\vec{b}}{|\vec{a}||\vec{b}|}$计算投影(垂直分解)
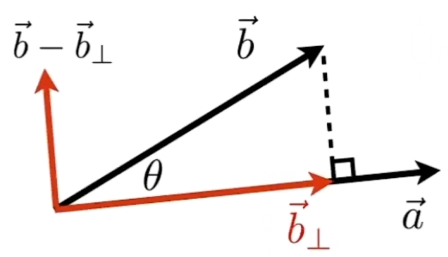
判断两向量方向
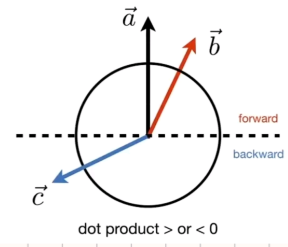
$\vec{a}\cdot\vec{b}\cases{>0 \Rightarrow同向\=0 \Rightarrow垂直\<0 \Rightarrow逆向}$
1.2.3 叉乘
几何学
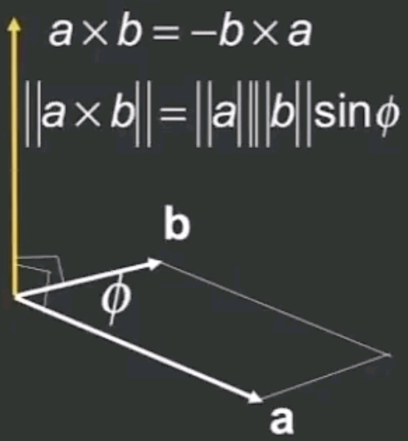
右手螺旋定则确认新向量方向
适用规则:交换律:$\vec{a}\times\vec{b}=-\vec{b}\times\vec{a}$
分配律:$\vec{a}\times(\vec{b}+\vec{c})=\vec{a}\times\vec{b}+\vec{a}\times\vec{c}$
结合律:$\vec{a}\times(k\vec{b})=k(\vec{a}\times\vec{b})$
零向量:$\vec{a}\times\vec{a}=\vec{0}$
数学
$\vec{a}\times\vec{b}=\pmatrix{y_az_b-y_bz_a\z_ax_b-x_az_b\x_ay_b-y_ax_b}=A*b=\pmatrix{0&-a_a&y_a\z_a&0&-x_a\-y_a&x_a&0}\pmatrix{x_b\y_b\z_b}$
A是$\vec{a}$的特征矩阵
运算结果:新向量
应用:
- 构建坐标系
- 右手坐标系(教学用):$\vec{x}\times\vec{y}=\vec{z}$
- 左手坐标系(生产用):$\vec{x}\times\vec{y}=-\vec{z}$
- 判断左右

$\vec{a}\times\vec{b}\cases{=+\vec{z}\Rightarrow\vec{b}在\vec{a}左侧\=-\vec{z}\Rightarrow\vec{b}在\vec{a}右侧}$ - 判断内外(法线、光栅化)

$\cases{\vec{AB}\times\vec{AP}\\vec{BC}\times\vec{BP}\\vec{CA}\times\vec{CP}}$- 若均在同侧则P在ABC外
- 否则P在ABC内
2.矩阵
2.1 矩阵运算
2.1.1 加法
$A_{(M\times N)}B_{(M\times N)}=C_{(M\times N)}$
$A+B=\pmatrix{a_{11}&a_{12}\a_{21}&a_{22}}+\pmatrix{b_{11}&b_{12}\b_{21}&b_{22}}=\pmatrix{a_{11}+b_{11}&a_{12}+b_{12}\a_{21}+b_{21}&a_{22}+b_{22}}=C$
$C_{xy}=A_{xy}=B_{xy}$
2.1.2 乘法
2.1.2.1 矩阵x数字
$A\times k=\pmatrix{a_{11}&a_{12}\a_{21}&a_{22}}\times k=\pmatrix{ka_{11}&ka_{12}\ka_{21}&ka_{22}}$
2.1.2.2 矩阵x矩阵
M行N列矩阵 X N行P列矩阵 = M行P列矩阵
$A_{(M\times N)}B_{(N\times P)}=C_{(M\times P)}$
$C_{xy}=A_x\cdot B_y$
例:
$\pmatrix{1&3\5&2\0&4}\pmatrix{3&6&9&4\2&7&8&3}=\pmatrix{9&27&33&13\19&44&61&26\8&28&32&12}$
$26=\pmatrix{5&2}\cdot \pmatrix{4\3}=20+6=26$
适用规则:
- 交换律:$AB \not = BA$
- 结合律:$(AB)C=A(BC)$
- 分配律:$A(B+C)=AB+AC$
2.1.2.3 矩阵x向量
要求:向量必须是列向量才有意义
$A_{(N\times M)}B_{(M\times 1)}=C_{(N\times 1)}$
用途:向量变换
例:向量y轴镜像(翻转x)
$\pmatrix{-1&0\0&1}\vec{a}=\pmatrix{-1&0\0&1}\pmatrix{x\y}=\pmatrix{-x\y}$
2.1.2.4 向量运算与矩阵运算的转换
点乘:
$\vec{a}\cdot\vec{b}=\vec{a}^T\vec{b}=\pmatrix{x_a&y_a&z_a}\pmatrix{x_b\y_b\z_b}=(x_ax_b+y_ay_b+z_az_b)$
叉乘:
$\vec{a}\times\vec{b}=A^*b=\pmatrix{0&-z_a&y_a\z_a&0&-x_a\-y_a&x_a&0}\pmatrix{x_b\y_b\z_b}$
2.1.3 转置
$A_{(M\times N)}^T=A_{(N\times M)}$
$\pmatrix{a_{11}&a_{12}\a_{21}&a_{22}\a_{31}&a_{32}}^T=\pmatrix{a_{11}&a_{21}&a_{31}\a_{12}&a_{22}&a_{32}}$
特性:$(AB)^T=B^TA^T$
2.2 单位矩阵与逆矩阵
2.2.1单位矩阵
单位矩阵是一个对角阵
$I_{3\times 3}=\pmatrix{1&0&0\0&1&0\0&0&1}$
任何矩阵乘单位矩阵不产生变化
$AI=IA=A$
2.2.2 逆矩阵
若$AB=I$则AB互为逆矩阵,B可记为$A^{-1}$
$AA^{-1}=A^{-1}A=I$
$(AB)^{-1}=B^{-1}A^{-1}$
3. 变换
3.1 2D变换
3.1.1 常见变换
缩放(Scale):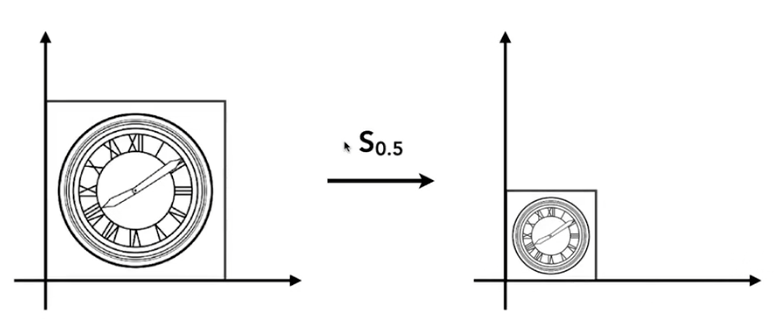
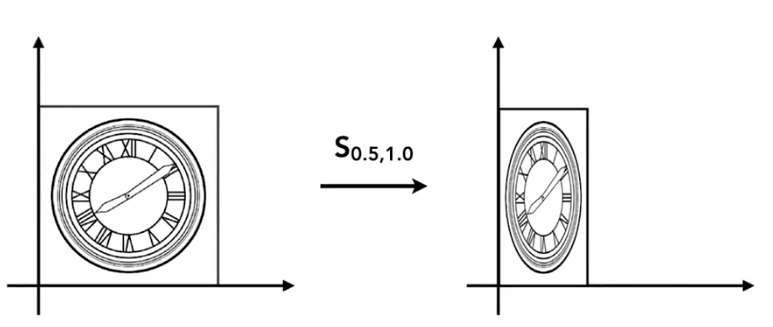
公式推导:
$\cases{x’=s_xx\y’=s_yy}\Rightarrow\pmatrix{x’\y’}=\pmatrix{s_x&0\0&s_y}\pmatrix{x\y}$
线性变换:
$S(s_x,s_y)=\pmatrix{s_x&0\0&s_y}$
齐次变换:
$S(s_x,s_y)=\pmatrix{s_x&0&0\0&s_y&0\0&0&1}\cdot\pmatrix{x\y\1}$
镜像(Reflection):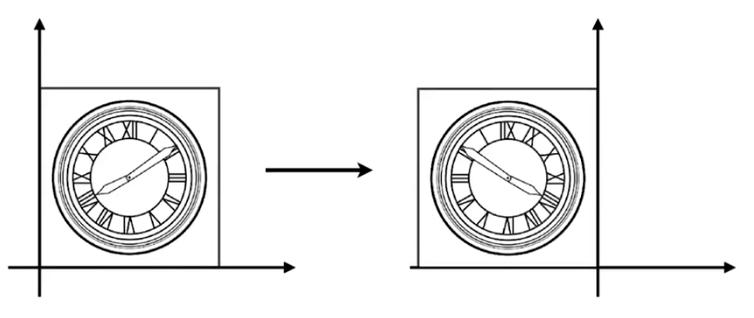
公式推导:
$\cases{x’=-x\y’=y}\Rightarrow\pmatrix{x’\y’}=\pmatrix{-1&0\0&1}\pmatrix{x\y}$
线性变换:
$\pmatrix{-1&0\0&1}$
齐次变换:
$\pmatrix{-1&0&0\0&1&0\0&0&1}$
切变(Shear):
$\cases{x’=ay\y’=y}\Rightarrow\pmatrix{x’\y’}=\pmatrix{1&a\0&1}\pmatrix{x\y}$
线性变换:
$\pmatrix{1&a\0&1}$
齐次变换:
$\pmatrix{1&a&0\0&1&0\0&0&1}$
旋转(Rotate):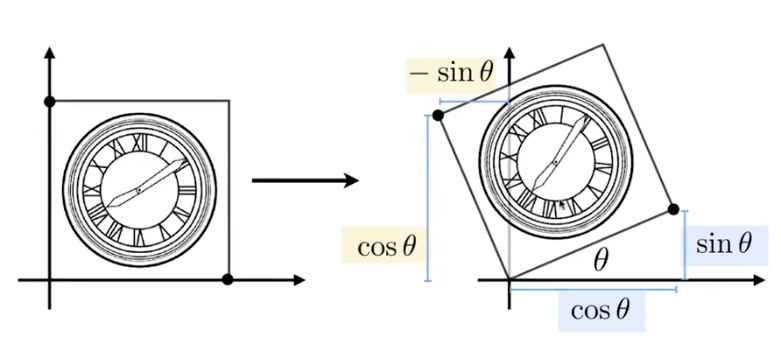
公式推导: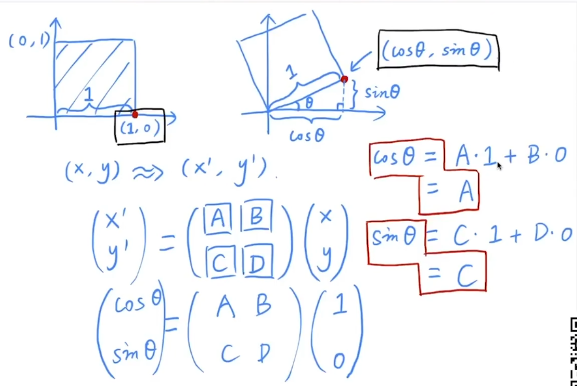
线性变换:
$R_\theta=\pmatrix{cos\theta&-sin\theta\sin\theta&cos\theta}$
齐次变换:
$R_\theta=\pmatrix{x’\y’\1}=\pmatrix{cos\theta&-sin\theta&0\sin\theta&cos\theta&0\0&0&1}\cdot\pmatrix{x\y\1}$
平移(Move):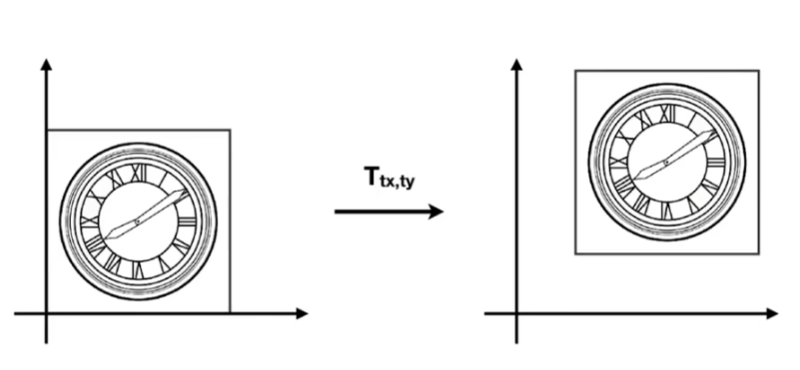
公式推导:
$\cases{x’=x+t_x\y’=y+t_y}\Rightarrow\pmatrix{x’\y’}=\pmatrix{a&b\c&d}\pmatrix{x\y}+\pmatrix{t_x\t_y}\Rightarrow\pmatrix{x’\y’\1}=\pmatrix{a&b&t_x\c&d&t_y\0&0&1}\cdot\pmatrix{x\y\1}$
线性变换:
$T(t_x,t_y)=\pmatrix{x’\y’}=\pmatrix{1&0\0&1}\pmatrix{x\y}+\pmatrix{t_x\ t_y}$
齐次变换:
$T(t_x,t_y)=\pmatrix{x’\y’\1}=\pmatrix{1&0&t_x\0&1&t_y\0&0&1}\cdot\pmatrix{x\y\1}$
3.1.2 常见变换矩阵速查表
| 变换名称 | 线性变换矩阵 | 齐次变换矩阵 |
|---|---|---|
| 缩放(Scale) | $S(s_x,s_y)=\pmatrix{s_x&0\0&s_y}$ | $S(s_x,s_y)=\pmatrix{s_x&0&0\0&s_y&0\0&0&1}\cdot\pmatrix{x\y\1}$ |
| 镜像(Reflection) | $\pmatrix{-1&0\0&1}$ | $\pmatrix{-1&0&0\0&1&0\0&0&1}$ |
| 切变(Shear) | $\pmatrix{1&a\0&1}$ | $\pmatrix{1&a&0\0&1&0\0&0&1}$ |
| 旋转(Rotate) | $R_\theta=\pmatrix{cos\theta&-sin\theta\sin\theta&cos\theta}$ | $R_\theta=\pmatrix{x’\y’\1}=\pmatrix{cos\theta&-sin\theta&0\sin\theta&cos\theta&0\0&0&1}\cdot\pmatrix{x\y\1}$ |
| 平移(Move) | $T(t_x,t_y)=\pmatrix{x’\y’}=\pmatrix{1&0\0&1}\pmatrix{x\y}+\pmatrix{t_x\ t_y}$ | $T(t_x,t_y)=\pmatrix{x’\y’\1}=\pmatrix{1&0&t_x\0&1&t_y\0&0&1}\cdot\pmatrix{x\y\1}$ |
3.1.2 线性变换(linear transform)范式
只要能将变换推导为以下形式的矩阵,就称之为线性变换
$\cases{x’=ax+by\y’=cx+dy}\Rightarrow\pmatrix{x’\y’}=\pmatrix{a&b\c&d}\pmatrix{x\y}$
缩放、镜像、切变、旋转都是线性变换
3.1.3 齐次坐标
平移的变换矩阵推导:
$\cases{x’=x+t_x\y’=y+t_y}\Rightarrow\pmatrix{x’\y’}=\pmatrix{a&b\c&d}\pmatrix{x\y}+\pmatrix{t_x\t_y}$
平移不是线性变换
需要一种方法可以简单的表达所有变换:齐次坐标
维度扩展:2维扩3维:
点:$(x,y,1)^T$
$\pmatrix{x\y\w}=\pmatrix{x/w\y/w\1},w\not=0$向量:$(x,y,0)^T$
向量具有平移不变性,所以是0
$\pmatrix{x’\y’\w’}=\pmatrix{1&0&t_x\0&1&t_y\0&0&1}\cdot\pmatrix{x\y\z}=\pmatrix{x+t_x\y+t_y\1}$向量+向量=向量
点-点=向量
点+向量=点
点+点=无意义,在齐次坐标下扩充为两点中点
$\pmatrix{a&b&t_x\c&d&t_y\0&0&1}\cdot\pmatrix{x\y\1}$