数据结构-堆

1. 堆的简介

堆的常用方法：

  • 构建优先队列
  • 支持堆排序
    堆排序
  • 快速找出一个集合中的最小值（或者最大值）

堆分为两种：

  • 最大堆(大顶堆)
    父节点的值比每一个子节点的值都要大
    根节点总是最大值
    可以用于降序排序
  • 最小堆(小顶堆)
    父节点的值比每一个子节点的值都要小
    根节点总是最小值
    可用于升序排序

例子：

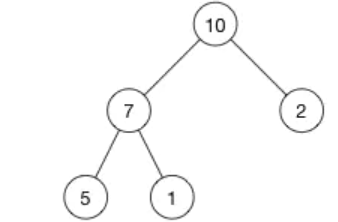
image-20211002013943710

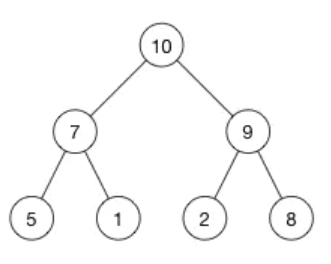
这是一个最大堆，，因为每一个父节点的值都比其子节点要大。10 比 7 和 2 都大。7 比 5 和 1都大。

注意：
堆的根节点中存放的是最大或者最小元素，但是其他节点的排序顺序是未知的。
在一个最大堆中，最大的那一个元素总是位于 index 0 的位置，但是最小的元素则未必是最后一个元素。
唯一能够保证的是最小的元素是一个叶节点，但是不确定是哪一个。

2. 堆和树的区别

堆并不能取代二叉搜索树，它们之间有相似之处也有一些不同。
我们来看一下两者的主要差别：

  • 节点的顺序

    • 二叉搜索树中，左子节点必须比父节点小，右子节点必须必比父节点大。

    • 在最大堆中两个子节点都必须比父节点小，而在最小堆中，它们都必须比父节点大。

  • 内存占用

    • 普通树占用的内存空间比它们存储的数据要多，必须为节点对象以及左/右子节点指针分配内存。
    • 堆仅仅使用一个数据来存储数组，且不使用指针。

  • 平衡

    • 二叉搜索树必须是“平衡”的情况下，其大部分操作的复杂度才能达到**O(log n)**。
    • 堆实际上不需要整棵树都是有序的。我们只需要满足堆属性即可，所以在堆中平衡不是问题。
      因为堆中数据的组织方式可以保证O(log n) 的性能。

  • 搜索

    • 在二叉树中搜索会很快
    • 但是在堆中搜索会很慢
      在堆中搜索不是第一优先级，因为使用堆的目的是将最大（或者最小）的节点放在最前面，从而快速的进行相关插入、删除操作。

3. 堆的存储(数组)

用数组来实现树相关的数据结构也许看起来有点古怪，但是它在时间和空间上都是很高效的。

我们准备将上面例子中的树这样存储：

1
[ 10, 7, 2, 5, 1 ]

就这么多！我们除了一个简单的数组以外，不需要任何额外的空间。

3.1 索引公式

节点在数组中的位置index 和它的父节点以及子节点的索引之间有一个映射关系。
如果 i 是节点的索引，那么下面的公式就给出了它的父节点和子节点在数组中的位置：

基础公式：

  • parent(i) = (i - 1) // 2
  • left(i) = 2i + 1
  • right(i) = 2i + 2

使用公式时需要注意：

  • right(i) 就是简单的 left(i) + 1
    左右节点总是处于相邻的位置。
  • 根节点(10)没有父节点，因为 -1 不是一个有效的数组索引。
    同样，节点 (2)，(5)和(1) 没有子节点，因为这些索引已经超过了数组的大小
    所以我们在使用这些索引值的时候需要保证是有效的索引值。

这些公式允许我们不使用指针就可以找到任何一个节点的父节点或者子节点。

3.2 节点数公式

理解数组索引和节点位置之间的关系非常重要。
这里有一个更大的堆，它有15个节点被分成了4层：

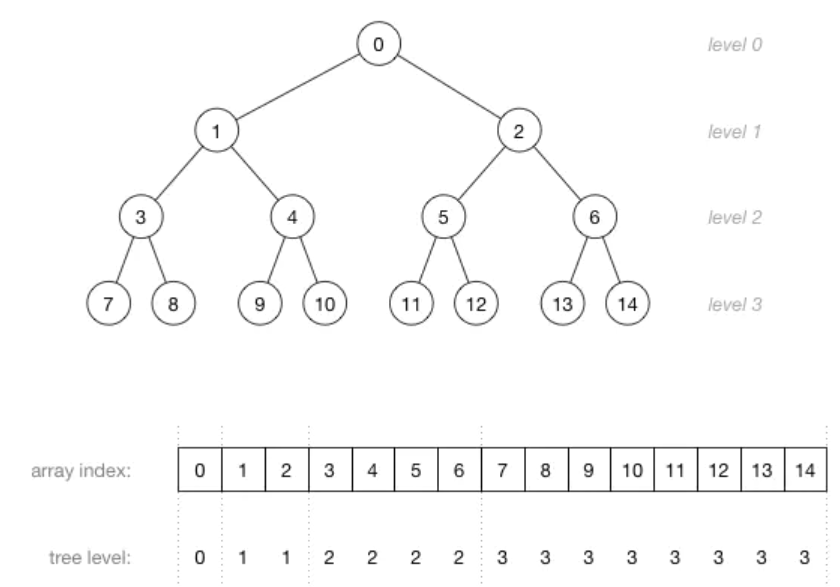
image-20211002013923396

由上图可以看到，数组中父节点总是在子节点的前面。

公式:

  • 如果一个堆有 n 个节点，那么它的高度是

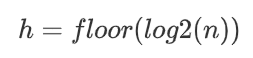
​ image-20211002160854520

这是因为我们总是要将这一层完全填满以后才会填充新的一层。
上面的例子有 15 个节点，所以它的高度是 floor(log2(15)) = floor(3.91) = 3。

如果最下面的一层已经填满，那么那一层包含 2^h 个节点。

  • 树中这一层以上所有的节点数目为

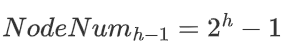
    ​ image-20211002160918051

同样是上面这个例子，最下面的一层有8个节点，实际上就是 2^3 = 8。
前面的三层一共包含7的节点，即：2^3 - 1 = 8 - 1 = 7。

  • 所以整个堆中的节点数目为：

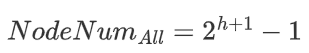
    ​ image-20211002160929502

上面的例子中，2^4 - 1 = 16 - 1 = 15

叶节点总是位于数组的 n//2 和 n-1 之间

注意：
你可以在普通二叉树中按照下面的方式组织数据，但是在堆中不可以：

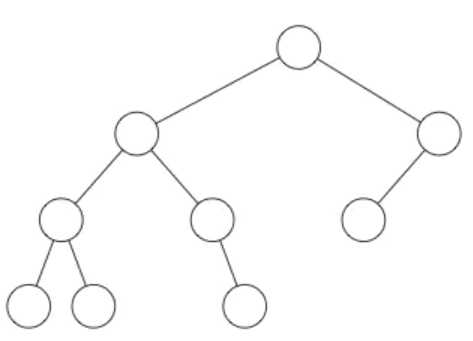
image-20211002014009799

在堆中，在当前层级所有的节点都已经填满之前不允许开是下一层的填充，所以堆总是有这样的形状：

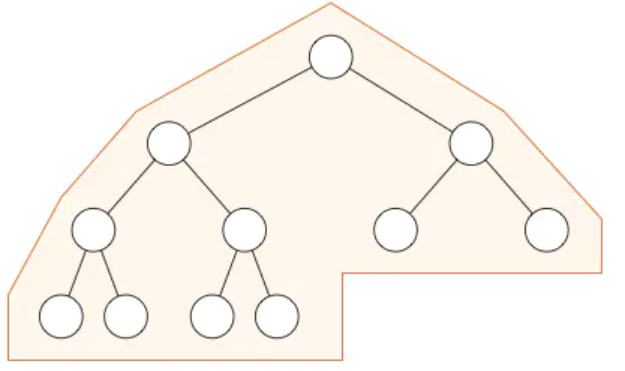
image-20211002014025394

注意：

  • 你可以使用普通树来模拟堆，但是那对空间是极大的浪费。
  • 并不是每一个堆都是一个有序数组！要将堆转换成有序数组，需要使用堆排序。

4. 堆的常用操作

有两个原始操作用于保证插入或删除节点以后堆是一个有效的最大堆或者最小堆：

  • shiftUp():
    如果一个节点比它的父节点大（最大堆）或者小（最小堆），那么需要将它同父节点交换位置。
    这样是这个节点在数组的位置上升。
  • shiftDown():
    如果一个节点比它的子节点小（最大堆）或者大（最小堆），那么需要将它向下移动。
    这个操作也称作“堆化（heapify）”。

shiftUp 或者 shiftDown 是一个递归的过程，所以它的时间复杂度是 **O(log n)**。

基于这两个原始操作还有一些其他的操作：

  • peek() ：
    不用删除节点就返回最大值（最大堆）或者最小值（最小堆）。
    时间复杂度 O(1) 。

  • insert(value):
    在堆的尾部添加一个新的元素，然后使用 shiftUp 来修复对。

  • remove():
    移除并返回最大值（最大堆）或者最小值（最小堆）。
    为了将这个节点删除后的空位填补上，需要将最后一个元素移到根节点的位置，然后使用 shiftDown 方法来修复堆。

  • removeAtIndex(index):
    和 remove() 一样，差别在于可以移除堆中任意节点，而不仅仅是根节点。
    当它与子节点比较位置不时无序时使用 shiftDown()，如果与父节点比较发现无序则使用 shiftUp()。

  • replace(index, value)：
    将一个更小的值（最小堆）或者更大的值（最大堆）赋值给一个节点。
    由于这个操作破坏了堆属性，所以需要使用 shiftUp() 来修复堆属性。

上面所有的操作的时间复杂度都是 **O(log n)**，因为 shiftUp 和 shiftDown 都很费时。

还有少数一些操作需要更多的时间：

  • search(value):
    堆不是为快速搜索而建立的，但是 replace() 和 removeAtIndex() 操作需要找到节点在数组中的index，所以你需要先找到这个index。
    时间复杂度：**O(n)**。
  • buildHeap(array):
    通过反复调用 insert() 方法将一个（无序）数组转换成一个堆。
    如果你足够聪明，你可以在 O(n) 时间内完成。
  • 堆排序：
    由于堆就是一个数组，我们可以使用它独特的属性将数组从低到高排序。
    时间复杂度：**O(n lg n)**。

注意：
到目前为止，堆的常用操作还是使用 insert() 插入一个新的元素，和通过 remove()移除最大或者最小值。
两者的时间复杂度都是**O(log n)**。
其其他的操作是用于支持更高级的应用，比如说建立一个优先队列。

4.1 插入

我们通过一个插入例子来看看插入操作的细节。
我们将数字 16 插入到这个堆中：

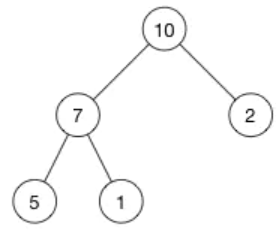
image-20211002014040987

堆的数组是： [ 10, 7, 2, 5, 1 ]。

第一股是将新的元素插入到数组的尾部。
数组变成：[ 10, 7, 2, 5, 1, 16 ]

相应的树变成了：

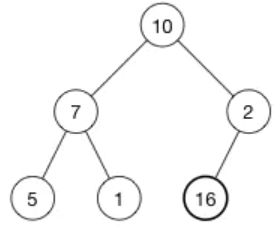
image-20211002014105489

16 被添加最后一行的第一个空位。

不行的是，现在堆属性不满足，因为 2 在 16 的上面，我们需要将大的数字在上面（这是一个最大堆）
为了恢复堆属性，我们需要交换 16 和 2。

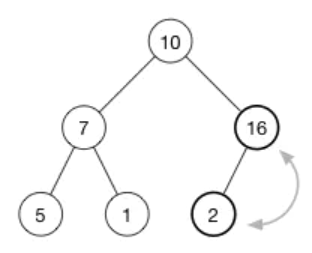
image-20211002014115401

现在还没有完成，因为 10 也比 16 小。
我们继续交换我们的插入元素和它的父节点，直到它的父节点比它大或者我们到达树的顶部。
这就是所谓的 shift-up，每一次插入操作后都需要进行。
它将一个太大或者太小的数字“浮起”到树的顶部。

最后我们得到的堆：

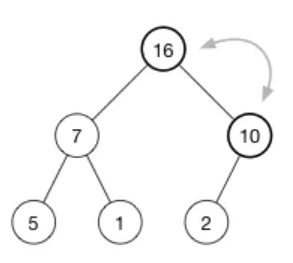
image-20211002014125610

现在每一个父节点都比它的子节点大。

4.2 删除根节点

我们将这个树中的 (10) 删除：

image-20211002014040987

现在顶部有一个空的节点，怎么处理？

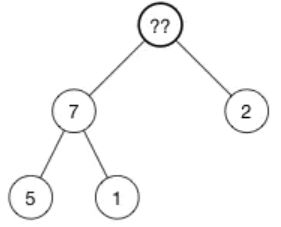
image-20211002014148719

当插入节点的时候，我们将新的值返给数组的尾部。现在我们来做相反的事情：我们取出数组中的最后一个元素，将它放到树的顶部，然后再修复堆属性。

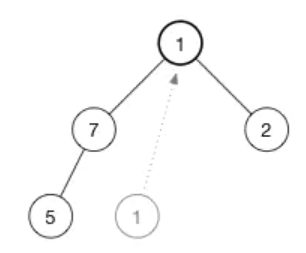
image-20211002014158542

现在来看怎么 shift-down (1)。为了保持最大堆的堆属性，我们需要树的顶部是最大的数据。现在有两个数字可用于交换 7 和 2。我们选择这两者中的较大者称为最大值放在树的顶部，所以交换 7 和 1，现在树变成了：

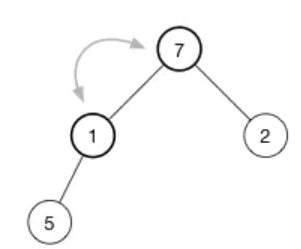
image-20211002014205304

继续堆化直到该节点没有任何子节点或者它比两个子节点都要大为止。对于我们的堆，我们只需要再有一次交换就恢复了堆属性：

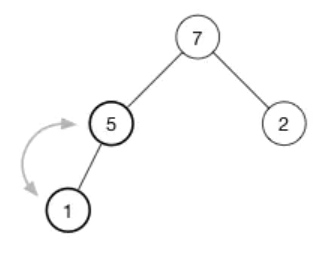
image-20211002014212991

4.3 删除任意节点

绝大多数时候你需要删除的是堆的根节点，因为这就是堆的设计用途。
但是，删除任意节点也很有用。

这是 remove() 的通用版本，它可能会使用到 shiftDown 和 shiftUp。

我们还是用前面的例子，删除 (7):

image-20211002014040987

对应的数组是：[ 10, 7, 2, 5, 1 ]

移除一个元素会破坏最大堆或者最小堆属性，我们需要将删除的元素和最后一个元素交换：
[ 10, 1, 2, 5, 7 ]

最后一个元素就是我们需要返回的元素；然后调用 removeLast() 来将它删除。
(1) 比它的子节点小，所以需要 shiftDown() 来修复。

然而，shift down 不是我们要处理的唯一情况。也有可能我们需要 shift up。考虑一下从下面的堆中删除 (5) 会发生什么：

image-20211002014236057

5. 代码实现堆

python代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
class Heap:
    def __init__(self,isBigTop):
        self.heapList = list()
        self.isBigTop = isBigTop
    
    def getTop(self):
        if len(self.heapList) == 0:
            return None
        return self.heapList[0]

    def __swap(self,index1,index2):
        t = self.heapList[index1]
        self.heapList[index1] = self.heapList[index2]
        self.heapList[index2] = t

    def __shitfUp(self,index):
        while index > 0:
            if (self.heapList[(index-1)//2] < self.heapList[index] and self.isBigTop)\
                or\
                (self.heapList[(index-1)//2] > self.heapList[index] and not self.isBigTop):
                self.__swap((index-1)//2,index)
                index = (index-1)//2
            else: break

    def __shiftDown(self,index):
        if index*2+1 >= len(self.heapList):
            return
        if self.isBigTop:
            while index*2+1 < len(self.heapList):
                if self.heapList[index] < self.heapList[index*2+1] or\
                   self.heapList[index] < self.heapList[index*2+2]:
                    if index*2+2 >= len(self.heapList) or \
                       self.heapList[index*2+1] > self.heapList[index*2+2]:
                        self.__swap(index*2+1,index)
                        index = index*2+1
                    else:
                        self.__swap(index*2+2,index)
                        index = index*2+2
                else: break
        else:
            while index*2+1 < len(self.heapList):
                if self.heapList[index] > self.heapList[index*2+1] or\
                   self.heapList[index] > self.heapList[index*2+2]:
                    if index*2+2 >= len(self.heapList) or\
                       self.heapList[index*2+1] < self.heapList[index*2+2]:
                        self.__swap(index*2+1,index)
                        index = index*2+1
                    else:
                        self.__swap(index*2+2,index)
                        index = index*2+2
                else: break

    def push(self, num):
        self.heapList.append(num)
        self.__shitfUp(len(self.heapList) - 1)

    def pop(self, index):
        if len(self.heapList) == 0 or index < 0 or index > len(self.heapList)-1:
            return None
        if index == len(self.heapList)-1:
            return self.heapList.pop()
        self.__swap(index,len(self.heapList) - 1)
        output = self.heapList.pop()
        if index == 0:
            self.__shiftDown(0)
        else:
            pIndex = (index-1)//2
            lIndex = 2*index+1
            rIndex = lIndex + 1
            if pIndex >= 0:
                self.__shitfUp(index)
            if lIndex < len(self.heapList) or rIndex < len(self.heapList):
                self.__shiftDown(index)
        return output

if __name__ == "__main__":
    numList = [ 10, 7, 2, 5, 1 ]
    h = Heap(True)
    h.heapList = numList
    h.push(10)
    print(h.heapList)