0. 概述

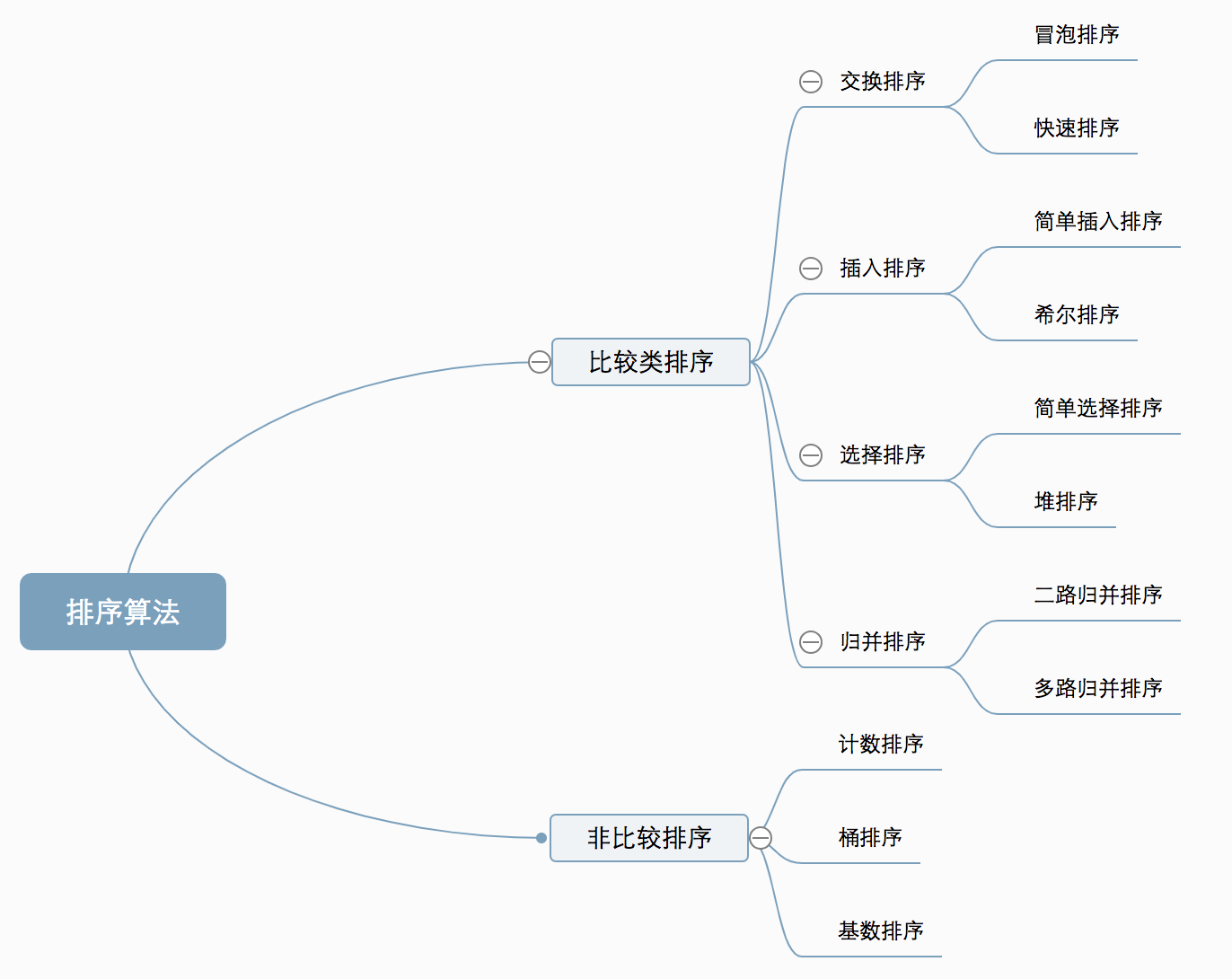
0.1 算法分类

十种常见排序算法可以分为两大类：

比较类排序：通过比较来决定元素间的相对次序，由于其时间复杂度不能突破O(nlogn)，因此也称为非线性时间比较类排序。
非比较类排序：不通过比较来决定元素间的相对次序，它可以突破基于比较排序的时间下界，以线性时间运行，因此也称为线性时间非比较类排序。

0.2 算法复杂度

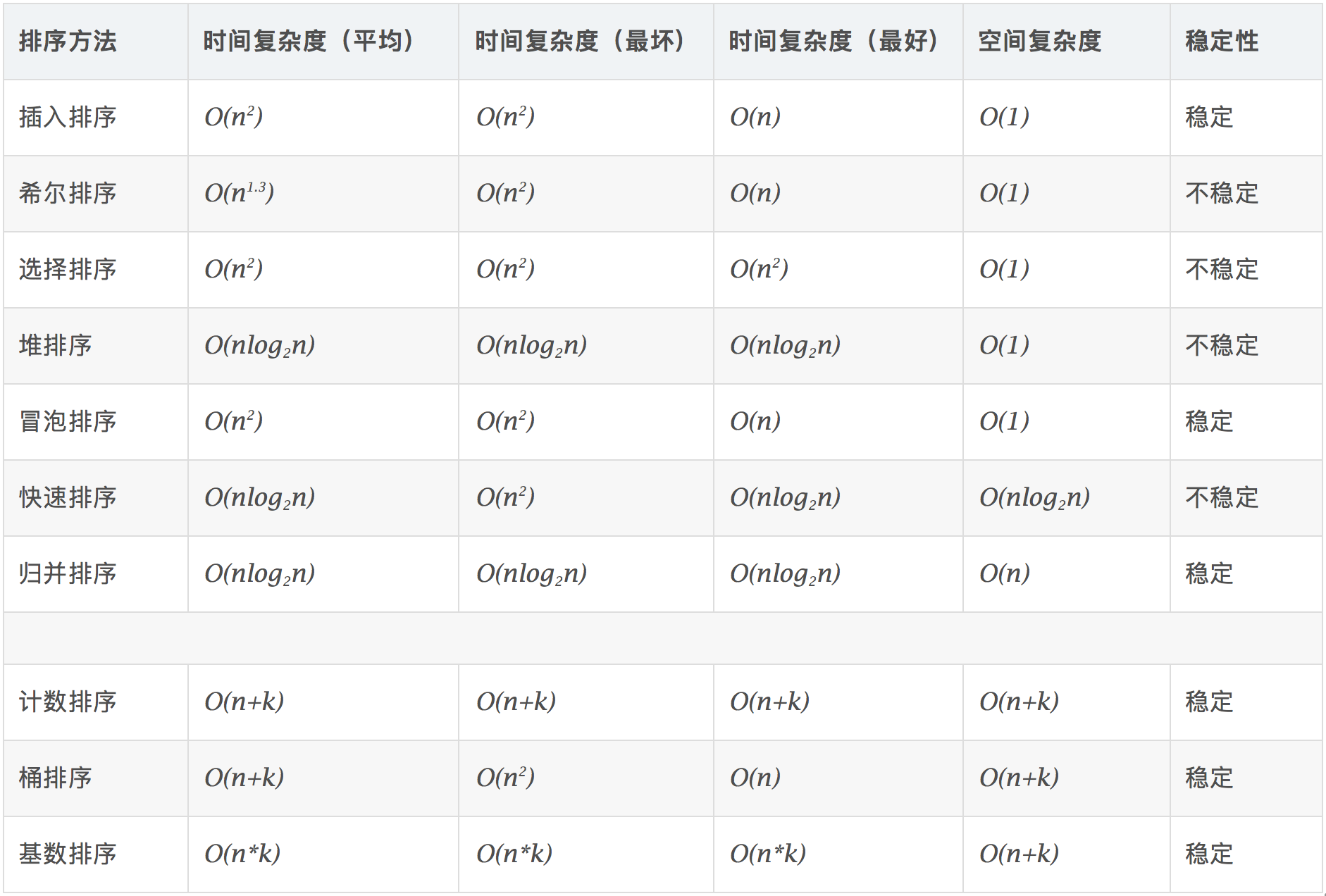
0.3 相关概念

稳定：如果a原本在b前面，而a=b，排序之后a仍然在b的前面。
不稳定：如果a原本在b的前面，而a=b，排序之后 a 可能会出现在 b 的后面。
时间复杂度：对排序数据的总的操作次数。反映当n变化时，操作次数呈现什么规律。
空间复杂度：是指算法在计算机

内执行时所需存储空间的度量，它也是数据规模n的函数。

1. 快速排序（Quick Sort）

1.1 算法描述

快速排序使用分治法来把一个串（list）分为两个子串（sub-lists）。具体算法描述如下：

从数列中挑出一个元素，称为 “基准”（pivot）；
重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

1.2 动图演示

快速排序img

1.3 代码实现

def quickSort(arr,left,right):
    if left >= right:
        return
    l = left
    r = right
    t = arr[l]
    while l < r:
        while l < r and arr[r] > t:
            r -= 1
        if l < r:
            arr[l] = arr[r]
            l += 1
        while l < r and arr[l] < t:
            l += 1
        if l < r:
            arr[r] = arr[l]
            r -= 1
    arr[l] = t
    quickSort(arr,left,l-1)
    quickSort(arr,l+1,right)

1.4 相关题型

剑指 Offer 45. 把数组排成最小的数

2. 归并排序（Merge Sort）

2.1 算法描述

归并排序是建立在归并操作上的一种有效的排序算法。

该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。

将已有序的子序列合并，得到完全有序的序列；
即先使每个子序列有序，再使子序列段间有序。
若将两个有序表合并成一个有序表，称为2-路归并。

把长度为n的输入序列分成两个长度为n/2的子序列；
对这两个子序列分别采用归并排序；
将两个排序好的子序列合并成一个最终的排序序列。

归并排序是一种稳定的排序方法。
和选择排序一样，归并排序的性能不受输入数据的影响，但表现比选择排序好的多，因为始终都是O(nlogn）的时间复杂度。

代价是需要额外的内存空间。

2.2 动图演示

归并排序img

2.3 代码实现

def mergeSort(arr):
    # 递归划分
    if len(arr) <= 1:
        return arr
    mid = len(arr)//2
    leftArr = mergeSort(arr[:mid])
    rightArr = mergeSort(arr[mid:])
	
    # 回溯治理
    mergeArr = list()
    while len(leftArr) != 0 or len(rightArr) != 0:
        if len(leftArr) == 0:
            while len(rightArr) != 0:
                mergeArr.append(rightArr.pop(0))
            break
        if len(rightArr) == 0:
            while len(leftArr) != 0:
                mergeArr.append(leftArr.pop(0))
            break
        if rightArr[0] > leftArr[0]:
            mergeArr.append(rightArr.pop(0))
        else:
            mergeArr.append(leftArr.pop(0))
    return mergeArr

2.4 相关题型

剑指 Offer 51. 数组中的逆序对

3. 堆排序（Heap Sort）

3.1 算法描述

堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。

关于堆的介绍请看：
数据结构-堆

堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：
即子结点的键值或索引总是小于（或者大于）它的父节点。

将初始待排序关键字序列(R1,R2….Rn)构建成大顶堆，此堆为初始的无序区；
将堆顶元素R[1]与最后一个元素R[n]交换，此时得到新的无序区(R1,R2,……Rn-1)和新的有序区(Rn),且满足R[1,2…n-1]<=R[n]；
由于交换后新的堆顶R[1]可能违反堆的性质，因此需要对当前无序区(R1,R2,……Rn-1)调整为新堆，然后再次将R[1]与无序区最后一个元素交换，得到新的无序区(R1,R2….Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1，则整个排序过程完成。

3.2 动图演示

堆排序img

3.3 代码实现

def swap(nums, indexA, indexB):
    t = nums[indexA]
    nums[indexA] = nums[indexB]
    nums[indexB] = t

def buildBigTopHeap(nums):
    index = (len(nums)-1) // 2
    for i in range(index,-1,-1):
        shiftDown(nums,i,len(nums))

def shiftDown(nums,index,lenth):
    leftP = index*2+1
    rightP = leftP+1
    if leftP >= lenth:
        return
    if rightP >= lenth:
        maxNum = nums[leftP]
    else:
        maxNum = max(nums[leftP], nums[rightP])
    if nums[index] < maxNum:
        if maxNum == nums[leftP]:
            swap(nums,index,leftP)
            shiftDown(nums,leftP,lenth)
        else:
            swap(nums,index,rightP)
            shiftDown(nums,rightP,lenth)

def incHeapSort(nums):
    buildBigTopHeap(nums)
    lenth = len(nums)
    while lenth > 1:
        lenth -= 1
        swap(nums,0,lenth)
        shiftDown(nums,0,lenth)

if __name__ == "__main__":
    nums = [16,7,3,20,17,8]
    incHeapSort(nums)
    print(nums)

3.4 相关题型

剑指 Offer 41. 数据流中的中位数

算法刷题

算法

数据结构-堆上一篇

动态规划下一篇