1. 简介

在数学中，几何向量（也称为欧几里得向量，通常简称向量、矢量），指具有大小和方向的量。

向量可以形象化地表示为带箭头的线段。

箭头所指：代表向量的方向；线段长度：代表向量的大小。

标量：只有大小,没有方向。

2. 向量的运算

2.1 基础运算

运算	描述
加减	各个分量分别相加减
数乘	向量与标量的乘数，可以对向量的长度进行缩放，如果标量>0，向量的方向不变，如果<0,向量的方向为反方向

2.2 点乘（点积）

两个向量点乘得到一个标量 ，数值等于两个向量长度相乘后再乘以二者夹角的余弦值 。
如果两个向量a,b均 为单位 向量 ,那么a.b等于向量b在向量a方向上的投影的长度

点乘后得到的是一个值

• 若结果 == 0，则 两向量 互垂直

• 若结果 < 0 ，则 两向量夹角大于90°

• 若结果 >0 ，则两向量夹角小于 90°

  

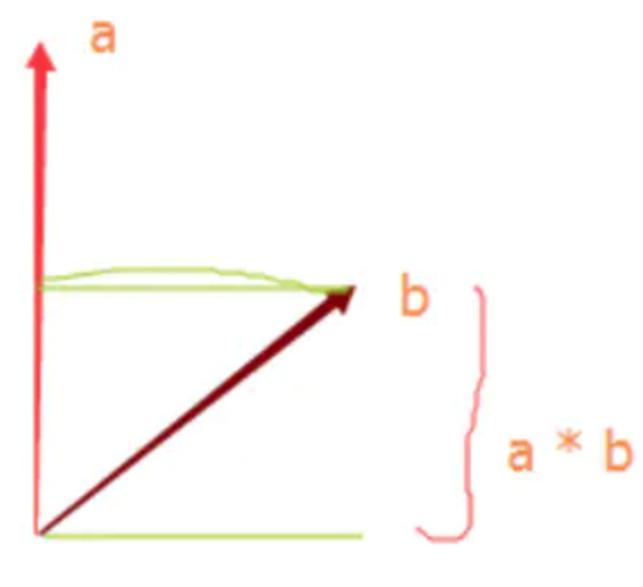
两个单位向量的点积得到两个向量的夹角的cos值，通过它可以知道两个向量的相似性。

利用点积可判断一个多边形是否面向摄像机还是背向摄像机。

如果点积越大，说明夹角越小，则物理离光照的轴线越近，光照越强。

2.3 叉乘

两个向量的叉乘得到一个新的向量，新向量垂直于原来两个向量，并且长度等于原向量长度相乘后再乘以夹角的正弦值，类似左手坐标系Z。

在Unity3D里面。两个向量的点乘所得到的是两个向量的余弦值，也就是-1 到1之间，0表示垂直，-1表示相反，1表示相同方向。

两个向量的叉乘所得到的是两个向量所组成的面的垂直向量，分两个方向。

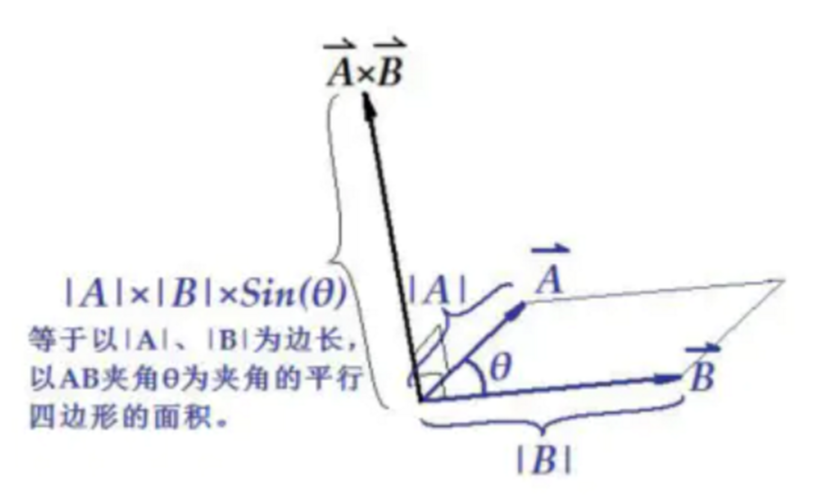
简单的说，点乘判断角度，叉乘判断方向。

形象的说当一个敌人在你身后的时候，叉乘可以判断你是往左转还是往右转更好的转向敌人，点乘得到你当前的面朝向的方向和你到敌人的方向的所成的角度大小。